从零开始的机器学习(前言)
最前
本文并不包括实际的算法说明,仅仅是这个系列的开端。
前言
前一段时间终于开始闲了下来,本来想到周边愉快的玩耍一番好好休息一下。但是朋友拜托做一个文本匹配和提取的工作,在小样本数据上初看都是些很规则的数据。但是在做模板测试的时候发现完全符合预期格式的占75%,基本符合的占24%,剩下的完全不匹配。之后就不停的修改模板和匹配规则想要适合所有格式,最后虽然结果是达到了,但是真的非常难看。然后才是真正的开始。
这其中比较严重的是本来非常严肃的文档,但是各种用措辞和句式却非常的随意。经过多次测试之后找了个最容易的实现–查表,但是随后却反而越来越在意,经过多次代码重构之后觉得用简单的文字和格式匹配几乎是无法实现的。于是我想起了之前写过的一些分类算法,然后结合一些自然语言处理工具处理那些格式混乱措辞随意甚至包括错字的文本。
分类算法
大约在两年前,我记得那时候网易云音乐突然出现在视野中,当时对它的推荐算法非常吃惊(现在的推荐似乎非常的奇怪)。而那时候我正好在做一个文本推荐工具,于是去专门了解的一些推荐算法,但是这里的关键问题还是分类算法。
分类算法大致有:k-近邻算法(kNN),决策树,朴素贝叶斯,支持向量机(SVM)等。其他的还有什么遗传算法,神经网络即使逻辑上看个八九不离十,但是实际看算法依旧云里雾里。
那个项目的流程是这样的,首先从网络抓取文本信息,文本可能是博客文章,新闻等。在进行文本相似度比较之后将相对质量较高的文本存入数据库,这里的相似度算法有TF-IDF和Jaccard等。然后使用k-NN和朴素贝叶斯等算法进行分类,k-NN由于非常容易理解和实现所以就偷懒用了(笑)。
k-近邻算法
实现上主要使用了,Python配合numpy库。其主要用到了欧式距离公式$d = \sqrt{(x_{1} - x_{2})^2 + (y_{1} - y_{2}) ^2}$,即两个向量点$(x_{1}, y_{1})$与$(x_{2}, y_{2})$之间的距离。假设有这样一组样本数据[[1.0, 1.2],[1, 1],[0, 0.2],[0, 0.1]]其对应两个分类[A, A, B, B]即A和B。那么假设存在这样一个点[0, 0],那么直观上说它可能属于分类B。首先观察分类A和B的区别,显然一类离原点近另外一类离原点比较远,直观上感觉打到点[0, 0]肯定离分类B比较近。如果样本量比较大或者分类比较多那么就不会有这种直观的感受了,这时候选择k-NN计算给出点到样本之间的距离。
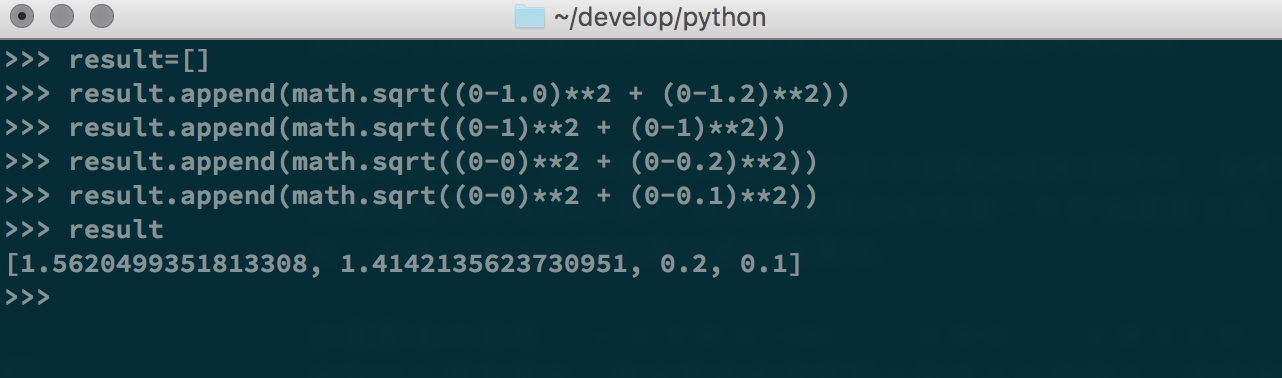
如上图非常直观的进行计算(顺便熟悉一下Python)代码,然后排序找出最短的距离再查表找到对应的点和其代表的类别就行了。
不得不说的是距离公式是可以扩展到多维空间的,比如两个点$[x_{1}, y_{1}, z_{1}, …, i_{1}]$和$[x_{2}, y_{2}, z_{2}, …, i_{2}]$,那么这个公式可以改写成
$d = \sqrt{(x_{1} - x_{2})^2 + (y_{1} - y_{2}) ^2 + (z_{1} - z_{2})^2 + … + (i_{1} -i_{2})^2}$
数学上定义的多维空间向量,在实际使用中就是从多个角度对数据的描述,或者说是特征值。而在实际中往往由于数据量和维度比较多,我们将每个样本数据都看做是一个多维向量,而每个样本分类就可以看做是一个多维矩阵。然后利用矩阵已知的算法和各种特性更加方便的进行计算,而这里使用numpy非常方便(最近看数学公式看的实在是遭不住了,在这就不献丑了)。当然这里缺点也是显而易见,在实际使用期间存在计算量过大的问题。
条件概率与贝叶斯
条件概率简单来说就假设A和B为某一样本中的两个事件P(A)和P(B)分别为A与B两个事件的发生的概率,而在B概率发生时A的概率使用P(A|B)表示,则有以下公式P(A|B)=P(B|A)*P(A)/P(B)。这个的核心在于从已知概率计算未知概率,这在实际生活中由于各种原因无法直接计算目标概率提供了非常有效的方法。比较直观的比如纸牌抽排,每当抽排之后剩余牌出现的概率都会随着已经抽出的牌进行变化。
| 关键词1 | 关键词2 | 类别 |
|---|---|---|
| 谷歌 | Android | 科技 |
| DeepMind | 星际争霸 | 学术 |
| 暴雪 | 星际争霸 | 娱乐 |
| Apple | 交互 | 设计 |
| TorchCraft | 学术 | |
| 谷歌 | AlphaGo | 科技 |
| 谷歌 | 病历 | 医疗 |
| 谷歌 | deepmind | 学术 |
如以上样本数据,为文章搞词频关键字和其对应的分类。实际的词频关键字为更多维度,并且存在一定的权重,此数据为样例没有实际意义。
此时获得一篇新的文章经过关键字提取计算之后的结果为(谷歌,星际争霸),那么这篇文章是学术文章的概率有多大,即求P(学术|谷歌x星际争霸)。根据条件概率公式可以将此问题转化为P(学术|谷歌x星际争霸)=P(谷歌x星际争霸|学术)xP(学术)/P(谷歌x星际争霸),经过一定的转换可以获得最终计算公式。
P(学术|谷歌x星际争霸)
= P(谷歌|学术) x P(星际争霸|学术) x P(学术)/(P(谷歌) x P(星际争霸))
上述公式解释为学术文章中存在谷歌关键字的概率乘学术文章中存在星际争霸的概率乘学术文章的概率除以全部文章中存在谷歌关键字的概率和全部文章中存在星际争霸的概率的乘积。那么带入公式P(学术|谷歌x星际争霸)=(1/3 * 1/3 * 3/8)/(4/8 * 2/8)=1/3。
由于数据比较简单我们可以看出,谷歌和星际争霸两个关键字在已有样本中并没有直接关系,但是在实际生活中我们可知,现实中是暴雪和deepmind可能存在于暴雪相关的娱乐报道,但是也有可能出自关于深度学习的学术文章。因此在实际情况中我们必定要有足够多的关键字,并且为某些关键字增加权重,比如文章来源等。
贝叶斯
接下来使用贝叶斯分类器,假设每篇文章存在n个特性(Feature)为F1,F2…Fn。现在存在m个分类(Category)为C1,C2…Cm。那么计算某新数据输入分类C的概率$P(C|F_{1}F_{2}…F_{n})=P(F_{1}F_{2}…F_{n}|C)P(C)/P(F_{1}F_{2}…F_{n})$,实际计算中对于所有分类来说分母为固定值,于是我们将其忽略并只关注等效的分子计算结果。而朴素贝叶斯又假设所有的F值相互独立互不影响那么上述等式等价于$P(F_{1}|C)P(F_{2}C)…P(F_{n}|C)P(C)$。
那么同上我们再次计算P(学术|谷歌x星际争霸)=P(谷歌|学术)P(星际争霸|学术)P(学术)=1/3 * 1/3 * 3/8=0.375。之后就是计算每一种分类的概率找出最大值。这种小样本完全体现不出有什么优势,同时可以试试调整样本的逻辑关系测试其对结果有多大影响。
推荐算法
对问题的解决自然有各种各样的途径,而每条途径的实现又有着千千万万的算法实现。推荐算法也是如此,并且推荐算法会直观的被感觉出来,因此实际中的推荐算法肯定是经过无数次调整测试并且结合多种算法的优缺点时下的。
推荐算法主要的思路分为两种,1、找到相似的用户然后在用户之间相互推荐。2、对推荐目标进行建模提取特征,之后给句用户是喜好推荐特征相似的目标。而现实中什么基于流行度、协同过滤等等思路也几乎差不多,有些相当简单粗暴而有些又有非常强的定制性和准确度。
而其中协同过滤是非常直观和有效的(其实是这个比较熟悉而已),也是用户间相互推荐的算法。
首先制作打分表
| 用户 | 物品A | 物品B | 物品C | 物品D |
|---|---|---|---|---|
| A | 1 | 0 | 1 | 0 |
| B | 0 | 1 | 0 | 1 |
| C | 1 | 0 | 1 | 1 |
打分表中三个用户A、B、C对四个物品进行打分,1为喜欢0未评价。由于数据非常简单,这里可以比较明确的看出A和C用户的相似度极高,那么就可以将A用户和C用户喜欢的物品相互推荐。并且在相似用户之间也可以根据其它用户的评分预测对新物品的评分,但是实际情况非常的复杂,对物品的评分也可能存在多个维度,权值的问题。而且用户相似度也不是仅仅看一下表就能确定的,其中也牵扯到各种算法…
机器学习
在我印象中很久之前最开始火的是AI,那时候虽然软硬件水平无法保障,但是这个人工智能的概念却火了一阵。然后经过很久的沉寂,莫名的神经网络又慢慢的兴起,但是那段时间相关资料依旧少的可怜。而现在以深度学习为契机,机器学习相关的内容又开始热了起来。最为关键的是随着互联网大数据的发展,各大公司的大力投入,给了我们些许的期待。但是目前的机器智能和我们通常所说的智能依旧不能相提并论,这不禁让人非常的失望。
就拿非常直观的聊天机器人来说,发现目前的资料和多年前初学编程的时候相差无几,依旧是各种预料的训练。唯一值得庆幸的是由于Python的兴起和各种开源库,目前从代码角度来说看起来似乎已经是水到渠成了。但是对于一个短期内想做一个聊天机器人来说,这几乎是不可能的。这整个过程由多道程序配合实现,目前几乎没有可用的全套实现,在不了解各个过程的实现原理的前提下,将各个只实现一部分功能的开源项目整合在一起,这难度可想而知。
在看了几天算法之后,觉得真是枯燥的受不了。幸好Python怎么写还没有忘记(虽然大多开始从Python2.7转向Python3.5),有实例程序跑起来还是非常的高兴的。
写在最后
机器学习也好,深度学习也好,还是没有捷径的。在折腾了一段时间后发现,还得老老实实回去复习数学知识,还得慢慢看各种算法。所以这个系列真的将是一个漫长的系列,当然了我做这些不是为了科研而是为了实际的使用,所以以实用为目的,不会是仅仅罗列枯燥的算法和概念的。
这是个不错的开始。